Hi!
I’m not sure how much background information I should provide as I’m new to this forum (and, as I’m sure is evident from the text below, fairly new to brms). I hope the below is sufficient!
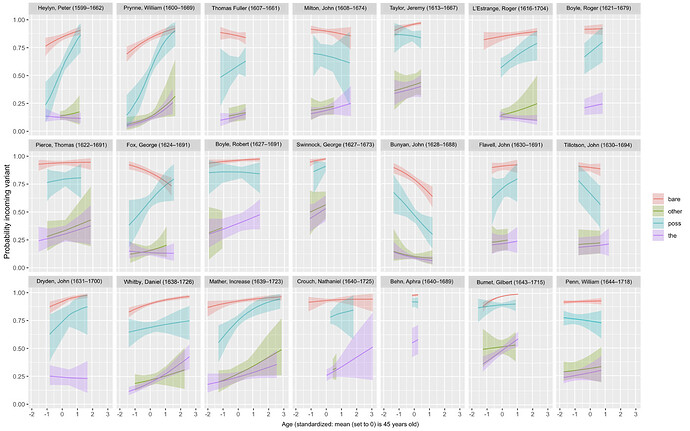
I’ve been running several models and have been doing an extensive comparison with WAIC and WAIC weights to ‘select’ the best model. The dependent variable is a linguistic variable (just binary: A or B), and the effect of age and determiner preceding the variant is assessed, with ‘individual’ as a group-level effect:
ing ~ det + age_sd + (det*age_sd|author) #M1
Another model of interest includes the effect of ‘isolation’ (whether or not an individual has spend time in isolation):
ing ~ det + age_sd + isolation + (det*age_sd|author) #M2
Inclusion of ‘isolation’ does not improve the fit (in fact, it increases the WAIC slightly and weights are in favour of the simpler model), but it does bring about a decrease in the sd(Intercept) of the Group-level effect author.
I’m trying to keep this short, so my question is: if you compare these models, can you conclude that M1 has more residual (author) variation than M2?
If so, what would be good practice wrt comparing them?
I’m also happy to hear tips for better techniques to implement this question! I’m not so much convinced that spending time in isolation affects the dependent variable, but I do think it helps reduce estimated variance in age slopes – if that makes sense?
Thanks in advance!