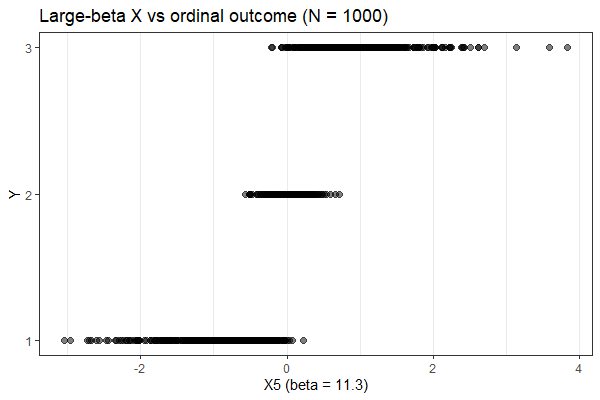
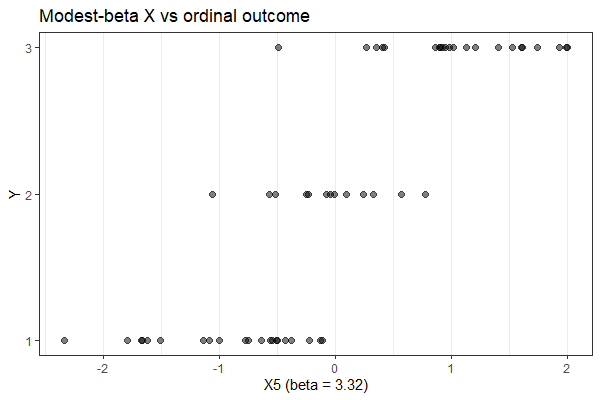
I tag here @Francesco_De_Vincentis because we are working with an ordinal regression and I noticed a strange behavior.
Let’s say we generate some data with the following model that simulates a regression with only a set of relevant variables:
data {
int<lower = 0> N; // number of observation
int<lower = 0> M; // number of predictors
int<lower = 1> K; // number of ordinal categories
vector[K-1] c; // cut points
}
transformed data {
real<lower = 0, upper = 1> sig_prob = 0.05;
}
generated quantities {
vector[M] beta; // slopes
matrix[N, M] X; // predictors
vector[N] mu;
int y[N];
for (m in 1:M) {
if (bernoulli_rng(sig_prob)) {
if (bernoulli_rng(0.5)) {
beta[m] = normal_rng(10, 1);
} else {
beta[m] = normal_rng(-10, 1);
}
} else {
beta[m] = normal_rng(0, 0.25);
}
}
for (n in 1:N) {
for (m in 1:M) {
X[n, m] = std_normal_rng(); // all predictors are mean centered and standardized
}
}
mu = X * beta;
for (n in 1:N) {
y[n] = ordered_logistic_rng(mu[n], c);
}
}
The parameters are fixed to
set.seed(123)
N = 56 # number of observations
M = 45 # number of predictors
K = 3 # number of ordinal categories
c = sort(runif(n = K - 1, min = -5, max = 5))
The generated slopes are the following:
[1] -0.233045611 -0.082993293 0.085635290 -0.135351220 -0.469997342
[6] 9.353118990 0.412084392 0.062155729 0.128925395 0.037598942
[11] 0.301502594 0.002788009 -0.075224657 -0.143522047 0.123930052
[16] 0.288065551 0.029104101 -0.023312894 -0.040097277 -0.174772110
[21] 9.476527099 0.008296223 -0.297025240 -0.221369662 -0.020534234
[26] 8.771793267 -12.259626932 0.456705693 0.185068152 -0.180819679
[31] -0.357336895 0.420012002 -0.048720008 -0.209211015 -0.014869948
[36] -0.237610720 -0.132745718 0.351899836 -0.151526916 -0.092970176
[41] 0.155793645 -0.210137725 -9.580069168 -0.413445021 0.067125648
then, I try to recover the parameters with the following model with very weak priors:
data {
int<lower = 0> N; // number of observation
int<lower = 0> M; // number of predictors
int<lower = 1> K; // number of ordinal categories
int<lower=1, upper=K> y[N]; // Observed ordinals
matrix[N, M] X; // predictors
}
parameters {
vector[M] beta; // slopes
ordered[K-1] c; // cut points
}
transformed parameters {
vector[N] mu = X * beta;
}
model {
c ~ std_normal();
beta ~ std_normal();
y ~ ordered_logistic(mu, c);
}
No fitting issues, but the retrieved betas are completely out-of scale:
[1] 0.55765983 -0.31872757 -0.01912787 -1.03558772 -0.11695698 1.61702316
[7] -0.16970714 -0.62116552 0.50572192 0.71391765 0.27750075 -0.42554441
[13] -0.15103297 0.30285230 -0.23127667 -0.08122528 1.20845964 0.47454160
[19] -0.48673457 0.67766070 1.47488536 -0.34840871 -0.93800531 -0.01341664
[25] 0.04542973 1.40791297 -2.13944193 0.28727535 0.33961248 0.65462492
[31] -0.08853437 0.35295322 -0.68077223 -0.47923495 -0.49212390 -0.25563038
[37] 0.38995377 -0.07001296 -0.86405367 0.21519595 0.24711355 -1.01672975
[43] -1.80061339 -0.30204615 -0.02697607
what am I doing wrong?