Adding interactive features significantly reduces the BFMI

zrn · February 27, 2024, 5:14am

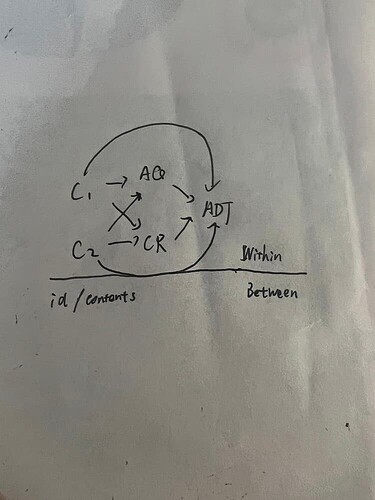
I am attempting to fit a Bayesian mediation model that includes two random factors. As shown in the diagram, c1 and c2 are independent variables (binary variables), aq and cr are mediator variables (continuous variables), and adt is the dependent variable (continuous variable). The model, which includes random intercepts and slopes, is currently performing well. On this basis, I want to introduce the interaction terms (c1*c2) to explore the impact of interactions on the dependent variable. However, upon adding the interaction terms, the Bayesian Fraction of Missing Information (BFMI) decreased from 0.66 to 0.08. I would like to understand the reasons behind this issue and how to address it.

zrn · February 27, 2024, 5:16am

zrn · February 27, 2024, 5:18am

without interaction：

random3="data{
int<lower=1> N;
vector[N] c1;
vector[N] c2;
vector[N] aq;
vector[N] cr;
vector[N] adt;
int<lower=1> J;
int<lower=1, upper=J> Group[N];
int<lower=1> G;
int<lower=1, upper=G> Group2[N];
}
parameters{
real alphaaq;
real beta1aq;
real beta2aq;
real<lower=0> sigma_alphaaq;
real<lower=0> sigma_beta1aq;
real<lower=0> sigma_beta2aq;
real<lower=0> sigmaaq;
real alphacr;
real beta1cr;
real beta2cr;
real<lower=0> sigma_alphacr;
real<lower=0> sigma_beta1cr;
real<lower=0> sigma_beta2cr;
real<lower=0> sigmacr;
real alphaadt;
real beta1adt;
real beta2adt;
real beta3adt;
real beta4adt;
real<lower=0> sigma_alphaadt;
real<lower=0> sigma_beta1adt;
real<lower=0> sigma_beta2adt;
real<lower=0> sigma_beta3adt;
real<lower=0> sigma_beta4adt;
real<lower=0> sigma_adt;
cholesky_factor_corr[11] Omega_chol1;
cholesky_factor_corr[11] Omega_chol2;
vector<lower=0>[11] sigma_ranef1;
vector<lower=0>[11] sigma_ranef2;
matrix[J,11] gamma1_raw;
matrix[G,11] gamma2_raw;
}
transformed parameters{
vector[J] gamma1alphaaq;
vector[J] gamma1alphacr;
vector[J] gamma1alpha;
vector[J] gamma1beta1aq;
vector[J] gamma1beta2aq;
vector[J] gamma1beta1cr;
vector[J] gamma1beta2cr;
vector[J] gamma1beta1adt;
vector[J] gamma1beta2adt;
vector[J] gamma1beta3adt;
vector[J] gamma1beta4adt;
vector[G] gamma2alphaaq;
vector[G] gamma2alphacr;
vector[G] gamma2alpha;
vector[G] gamma2beta1aq;
vector[G] gamma2beta2aq;
vector[G] gamma2beta1cr;
vector[G] gamma2beta2cr;
vector[G] gamma2beta1adt;
vector[G] gamma2beta2adt;
vector[G] gamma2beta3adt;
vector[G] gamma2beta4adt;
vector[N] mu_adt;
vector[N] mu_aq;
vector[N] mu_cr;
matrix[J, 11] gamma1 = gamma1_raw * diag_pre_multiply(sigma_ranef1, Omega_chol1)‘;
matrix[G, 11] gamma2 = gamma2_raw * diag_pre_multiply(sigma_ranef2, Omega_chol2)’;
for (j in 1:J){
gamma1alphaaq[j] = gamma1[j,1];
gamma1alphacr[j] = gamma1[j,2];
gamma1alpha[j]= gamma1[j,3];
gamma1beta1aq[j]= gamma1[j,4];
gamma1beta1cr[j]= gamma1[j,5];
gamma1beta1adt[j]= gamma1[j,6];
gamma1beta2aq[j]= gamma1[j,7];
gamma1beta2cr[j]= gamma1[j,8];
gamma1beta2adt[j]= gamma1[j,9];
gamma1beta3adt[j]= gamma1[j,10];
gamma1beta4adt[j]= gamma1[j,11];
}
for (g in 1:G) {
gamma2alphaaq[g] = gamma2[g,1];
gamma2alphacr[g] = gamma2[g,2];
gamma2alpha[g]= gamma2[g,3];
gamma2beta1aq[g]= gamma2[g,4];
gamma2beta1cr[g]= gamma2[g,5];
gamma2beta1adt[g]= gamma2[g,6];
gamma2beta2aq[g]= gamma2[g,7];
gamma2beta2cr[g]= gamma2[g,8];
gamma2beta2adt[g]= gamma2[g,9];
gamma2beta3adt[g]= gamma2[g,10];
gamma2beta4adt[g]= gamma2[g,11];
}
for (n in 1:N) {
mu_aq[n] = alphaaq + gamma1alphaaq[Group[n]] + gamma2alphaaq[Group2[n]]+
(beta1aq+gamma1beta1aq[Group[n]]+gamma2beta1aq[Group2[n]]) * c1[n] +
(beta2aq+gamma1beta2aq[Group[n]]+gamma2beta2aq[Group2[n]]) * c2[n];
mu_cr[n] = alphacr + gamma1alphacr[Group[n]] + gamma2alphacr[Group2[n]]+
(beta1cr+gamma1beta1cr[Group[n]]+gamma2beta1cr[Group2[n]]) * c1[n] +
(beta2cr+gamma1beta2cr[Group[n]]+gamma2beta2cr[Group2[n]]) * c2[n];
mu_adt[n] = alphaadt + gamma1alpha[Group[n]] + gamma2alpha[Group2[n]]+
(beta1adt+gamma1beta1adt[Group[n]]+gamma2beta1adt[Group2[n]]) * c1[n] +
(beta2adt+gamma1beta2adt[Group[n]]+gamma2beta2adt[Group2[n]]) * c2[n] +
(beta3adt+gamma1beta3adt[Group[n]]+gamma2beta3adt[Group2[n]]) * aq[n] +
(beta4adt+gamma1beta4adt[Group[n]]+gamma2beta4adt[Group2[n]]) * cr[n];
}
}
model{
sigma_alphaaq ~ student_t(5, 0, 2);
sigma_beta1aq ~ student_t(5, 0, 2);
sigma_beta2aq ~ student_t(5, 0, 2);
alphaaq ~ normal(0, sigma_alphaaq);
beta1aq ~ normal(0, sigma_beta1aq);
beta2aq ~ normal(0, sigma_beta2aq);
sigmaaq ~ student_t(5, 0, 2);
sigma_alphacr ~ student_t(5, 0, 2);
sigma_beta1cr ~ student_t(5, 0, 2);
sigma_beta2cr ~ student_t(5, 0, 2);
alphacr ~ normal(0, sigma_alphacr);
beta1cr ~ normal(0, sigma_beta1cr);
beta2cr ~ normal(0, sigma_beta2cr);
to_vector(gamma1_raw) ~ normal(0, 1);
to_vector(gamma2_raw) ~ normal(0, 1);
sigmacr ~ student_t(5, 0, 2);
sigma_alphaadt ~ student_t(5, 0, 2);
sigma_beta1adt ~ student_t(5, 0, 2);
sigma_beta2adt ~ student_t(5, 0, 2);
sigma_beta3adt ~ student_t(5, 0, 2);
sigma_beta4adt ~ student_t(5, 0, 2);
alphaadt ~ normal(0, sigma_alphaadt);
beta1adt ~ normal(0, sigma_beta1adt);
beta2adt ~ normal(0, sigma_beta2adt);
beta3adt ~ normal(0, sigma_beta3adt);
beta4adt ~ normal(0, sigma_beta4adt);
sigma_adt ~ student_t(5, 0, 2);
sigma_ranef1 ~ student_t(5, 0, 2);
sigma_ranef2 ~ student_t(5, 0, 2);
Omega_chol1 ~ lkj_corr_cholesky(2.0);
Omega_chol2 ~ lkj_corr_cholesky(2.0);
aq ~ normal(mu_aq, sigmaaq);
cr ~ normal(mu_cr, sigmacr);
adt ~ normal(mu_adt, sigma_adt);
}
generated quantities{
real naiveIndEffect1;
real naiveIndEffect2;
real naiveIndEffect3;
real naiveIndEffect4;
naiveIndEffect1=beta1aq * beta3adt;
naiveIndEffect2=beta1cr * beta4adt;
naiveIndEffect3=beta2aq * beta3adt;
naiveIndEffect4=beta2cr * beta4adt;
}
"

zrn · February 27, 2024, 5:20am

adding interaction:

random6="data{
int<lower=1> N;
vector[N] c1;
vector[N] c2;
vector[N] x;
vector[N] aq;
vector[N] cr;
vector[N] adt;
int<lower=1> J;
int<lower=1, upper=J> Group[N];
int<lower=1> G;
int<lower=1, upper=G> Group2[N];
}
parameters{
real alphaaq;
real beta1aq;
real beta2aq;
real beta3aq;
real<lower=0> sigma_alphaaq;
real<lower=0> sigma_beta1aq;
real<lower=0> sigma_beta2aq;
real<lower=0> sigma_beta3aq;
real<lower=0> sigmaaq;
real alphacr;
real beta1cr;
real beta2cr;
real beta3cr;
real<lower=0> sigma_alphacr;
real<lower=0> sigma_beta1cr;
real<lower=0> sigma_beta2cr;
real<lower=0> sigma_beta3cr;
real<lower=0> sigmacr;
real alphaadt;
real beta1adt;
real beta2adt;
real beta3adt;
real beta4adt;
real beta5adt;
real<lower=0> sigma_alphaadt;
real<lower=0> sigma_beta1adt;
real<lower=0> sigma_beta2adt;
real<lower=0> sigma_beta3adt;
real<lower=0> sigma_beta4adt;
real<lower=0> sigma_beta5adt;
real<lower=0> sigma_adt;
cholesky_factor_corr[14] Omega_chol1;
cholesky_factor_corr[14] Omega_chol2;
vector<lower=0>[14] sigma_ranef1;
vector<lower=0>[14] sigma_ranef2;
matrix[J,14] gamma1_raw;
matrix[G,14] gamma2_raw;
}
transformed parameters{
vector[J] gamma1alphaaq;
vector[J] gamma1alphacr;
vector[J] gamma1alpha;
vector[J] gamma1beta1aq;
vector[J] gamma1beta2aq;
vector[J] gamma1beta1cr;
vector[J] gamma1beta2cr;
vector[J] gamma1beta1adt;
vector[J] gamma1beta2adt;
vector[J] gamma1beta3adt;
vector[J] gamma1beta4adt;
vector[J] gamma1beta3aq;
vector[J] gamma1beta3cr;
vector[J] gamma1beta5adt;
vector[G] gamma2alphaaq;
vector[G] gamma2alphacr;
vector[G] gamma2alpha;
vector[G] gamma2beta1aq;
vector[G] gamma2beta2aq;
vector[G] gamma2beta1cr;
vector[G] gamma2beta2cr;
vector[G] gamma2beta1adt;
vector[G] gamma2beta2adt;
vector[G] gamma2beta3adt;
vector[G] gamma2beta4adt;
vector[G] gamma2beta3aq;
vector[G] gamma2beta3cr;
vector[G] gamma2beta5adt;
vector[N] mu_adt;
vector[N] mu_aq;
vector[N] mu_cr;
matrix[J, 14] gamma1 = gamma1_raw * diag_pre_multiply(sigma_ranef1, Omega_chol1)‘;
matrix[G, 14] gamma2 = gamma2_raw * diag_pre_multiply(sigma_ranef2, Omega_chol2)’;
for (j in 1:J){
gamma1alphaaq[j] = gamma1[j,1];
gamma1alphacr[j] = gamma1[j,2];
gamma1alpha[j]= gamma1[j,3];
gamma1beta1aq[j]= gamma1[j,4];
gamma1beta1cr[j]= gamma1[j,5];
gamma1beta1adt[j]= gamma1[j,6];
gamma1beta2aq[j]= gamma1[j,7];
gamma1beta2cr[j]= gamma1[j,8];
gamma1beta2adt[j]= gamma1[j,9];
gamma1beta3adt[j]= gamma1[j,10];
gamma1beta4adt[j]= gamma1[j,11];
gamma1beta3aq[j]= gamma1[j,12];
gamma1beta3cr[j]= gamma1[j,13];
gamma1beta5adt[j]= gamma1[j,14];
}
for (g in 1:G) {
gamma2alphaaq[g] = gamma2[g,1];
gamma2alphacr[g] = gamma2[g,2];
gamma2alpha[g]= gamma2[g,3];
gamma2beta1aq[g]= gamma2[g,4];
gamma2beta1cr[g]= gamma2[g,5];
gamma2beta1adt[g]= gamma2[g,6];
gamma2beta2aq[g]= gamma2[g,7];
gamma2beta2cr[g]= gamma2[g,8];
gamma2beta2adt[g]= gamma2[g,9];
gamma2beta3adt[g]= gamma2[g,10];
gamma2beta4adt[g]= gamma2[g,11];
gamma2beta3aq[g]= gamma2[g,12];
gamma2beta3cr[g]= gamma2[g,13];
gamma2beta5adt[g]= gamma2[g,14];
}
for (n in 1:N) {
mu_aq[n] = alphaaq + gamma1alphaaq[Group[n]] + gamma2alphaaq[Group2[n]]+
(beta1aq+gamma1beta1aq[Group[n]]+gamma2beta1aq[Group2[n]]) * c1[n] +
(beta2aq+gamma1beta2aq[Group[n]]+gamma2beta2aq[Group2[n]]) * c2[n]+
(beta3aq+gamma1beta3aq[Group[n]]+gamma2beta3aq[Group2[n]]) * x[n];
mu_cr[n] = alphacr + gamma1alphacr[Group[n]] + gamma2alphacr[Group2[n]]+
(beta1cr+gamma1beta1cr[Group[n]]+gamma2beta1cr[Group2[n]]) * c1[n] +
(beta2cr+gamma1beta2cr[Group[n]]+gamma2beta2cr[Group2[n]]) * c2[n]+
(beta3cr+gamma1beta3cr[Group[n]]+gamma2beta3cr[Group2[n]]) * x[n];
mu_adt[n] = alphaadt + gamma1alpha[Group[n]] + gamma2alpha[Group2[n]]+
(beta1adt+gamma1beta1adt[Group[n]]+gamma2beta1adt[Group2[n]]) * c1[n] +
(beta2adt+gamma1beta2adt[Group[n]]+gamma2beta2adt[Group2[n]]) * c2[n] +
(beta3adt+gamma1beta3adt[Group[n]]+gamma2beta3adt[Group2[n]]) * aq[n] +
(beta4adt+gamma1beta4adt[Group[n]]+gamma2beta4adt[Group2[n]]) * cr[n]+
(beta5adt+gamma1beta5adt[Group[n]]+gamma2beta5adt[Group2[n]]) * x[n];
}
}
model{
sigma_alphaaq ~ student_t(5, 0, 2);
sigma_beta1aq ~ student_t(5, 0, 2);
sigma_beta2aq ~ student_t(5, 0, 2);
sigma_beta3aq ~ student_t(5, 0, 2);
alphaaq ~ normal(0, sigma_alphaaq);
beta1aq ~ normal(0, sigma_beta1aq);
beta2aq ~ normal(0, sigma_beta2aq);
beta3aq ~ normal(0, sigma_beta3aq);
sigmaaq ~ student_t(5, 0, 2);
sigma_alphacr ~ student_t(5, 0, 2);
sigma_beta1cr ~ student_t(5, 0, 2);
sigma_beta2cr ~ student_t(5, 0, 2);
sigma_beta3cr ~ student_t(5, 0, 2);
alphacr ~ normal(0, sigma_alphacr);
beta1cr ~ normal(0, sigma_beta1cr);
beta2cr ~ normal(0, sigma_beta2cr);
beta3cr ~ normal(0, sigma_beta2cr);
to_vector(gamma1_raw) ~ normal(0, 1);
to_vector(gamma2_raw) ~ normal(0, 1);
sigmacr ~ student_t(5, 0, 2);
sigma_alphaadt ~ student_t(5, 0, 2);
sigma_beta1adt ~ student_t(5, 0, 2);
sigma_beta2adt ~ student_t(5, 0, 2);
sigma_beta3adt ~ student_t(5, 0, 2);
sigma_beta4adt ~ student_t(5, 0, 2);
sigma_beta5adt ~ student_t(5, 0, 2);
alphaadt ~ normal(0, sigma_alphaadt);
beta1adt ~ normal(0, sigma_beta1adt);
beta2adt ~ normal(0, sigma_beta2adt);
beta3adt ~ normal(0, sigma_beta3adt);
beta4adt ~ normal(0, sigma_beta4adt);
beta5adt ~ normal(0, sigma_beta5adt);
sigma_adt ~ student_t(5, 0, 2);
sigma_ranef1 ~ student_t(5, 0, 2);
sigma_ranef2 ~ student_t(5, 0, 2);
Omega_chol1 ~ lkj_corr_cholesky(2.0);
Omega_chol2 ~ lkj_corr_cholesky(2.0);
aq ~ normal(mu_aq, sigmaaq);
cr ~ normal(mu_cr, sigmacr);
adt ~ normal(mu_adt, sigma_adt);
}
generated quantities{
real naiveIndEffect1;
real naiveIndEffect2;
real naiveIndEffect3;
real naiveIndEffect4;
naiveIndEffect1=beta1aq * beta3adt;
naiveIndEffect2=beta1cr * beta4adt;
naiveIndEffect3=beta2aq * beta3adt;
naiveIndEffect4=beta2cr * beta4adt;
}
"

zrn · February 27, 2024, 5:23am

data.csv (84.6 KB)
My x is obtained by directly multiplying two binary variables (c1 and c2). Should I provide further description in rstan rather than doing it directly like this?
Here is the data I used. Looking forward to receiving a response！

Bob_Carpenter · February 27, 2024, 10:06pm

Here’s a slightly more readable version of the first model with indentation and syntax highlighting:

data{
  int<lower=1> N;
  vector[N] c1;
  vector[N] c2;
  vector[N] aq;
  vector[N] cr;
  vector[N] adt;
  int<lower=1> J;
  int<lower=1, upper=J> Group[N];
  int<lower=1> G;
  int<lower=1, upper=G> Group2[N];
}
parameters{
  real alphaaq;
  real beta1aq;
  real beta2aq;
  real<lower=0> sigma_alphaaq;
  real<lower=0> sigma_beta1aq;
  real<lower=0> sigma_beta2aq;
  real<lower=0> sigmaaq;
  real alphacr;
  real beta1cr;
  real beta2cr;
  real<lower=0> sigma_alphacr;
  real<lower=0> sigma_beta1cr;
  real<lower=0> sigma_beta2cr;
  real<lower=0> sigmacr;
  real alphaadt;
  real beta1adt;
  real beta2adt;
  real beta3adt;
  real beta4adt;
  real<lower=0> sigma_alphaadt;
  real<lower=0> sigma_beta1adt;
  real<lower=0> sigma_beta2adt;
  real<lower=0> sigma_beta3adt;
  real<lower=0> sigma_beta4adt;
  real<lower=0> sigma_adt;
  cholesky_factor_corr[11] Omega_chol1;
  cholesky_factor_corr[11] Omega_chol2;
  vector<lower=0>[11] sigma_ranef1;
  vector<lower=0>[11] sigma_ranef2;
  matrix[J,11] gamma1_raw;
  matrix[G,11] gamma2_raw;
}
transformed parameters{
  vector[J] gamma1alphaaq;
  vector[J] gamma1alphacr;
  vector[J] gamma1alpha;
  vector[J] gamma1beta1aq;
  vector[J] gamma1beta2aq;
  vector[J] gamma1beta1cr;
  vector[J] gamma1beta2cr;
  vector[J] gamma1beta1adt;
  vector[J] gamma1beta2adt;
  vector[J] gamma1beta3adt;
  vector[J] gamma1beta4adt;
  vector[G] gamma2alphaaq;
  vector[G] gamma2alphacr;
  vector[G] gamma2alpha;
  vector[G] gamma2beta1aq;
  vector[G] gamma2beta2aq;
  vector[G] gamma2beta1cr;
  vector[G] gamma2beta2cr;
  vector[G] gamma2beta1adt;
  vector[G] gamma2beta2adt;
  vector[G] gamma2beta3adt;
  vector[G] gamma2beta4adt;
  vector[N] mu_adt;
  vector[N] mu_aq;
  vector[N] mu_cr;
  matrix[J, 11] gamma1 = gamma1_raw * diag_pre_multiply(sigma_ranef1, Omega_chol1)‘;
  matrix[G, 11] gamma2 = gamma2_raw * diag_pre_multiply(sigma_ranef2, Omega_chol2)’;
  for (j in 1:J){
    gamma1alphaaq[j] = gamma1[j,1];
    gamma1alphacr[j] = gamma1[j,2];
    gamma1alpha[j]= gamma1[j,3];
    gamma1beta1aq[j]= gamma1[j,4];
    gamma1beta1cr[j]= gamma1[j,5];
    gamma1beta1adt[j]= gamma1[j,6];
    gamma1beta2aq[j]= gamma1[j,7];
    gamma1beta2cr[j]= gamma1[j,8];
    gamma1beta2adt[j]= gamma1[j,9];
    gamma1beta3adt[j]= gamma1[j,10];
    gamma1beta4adt[j]= gamma1[j,11];
  }
  for (g in 1:G) {
    gamma2alphaaq[g] = gamma2[g,1];
    gamma2alphacr[g] = gamma2[g,2];
    gamma2alpha[g]= gamma2[g,3];
    gamma2beta1aq[g]= gamma2[g,4];
    gamma2beta1cr[g]= gamma2[g,5];
    gamma2beta1adt[g]= gamma2[g,6];
    gamma2beta2aq[g]= gamma2[g,7];
    gamma2beta2cr[g]= gamma2[g,8];
    gamma2beta2adt[g]= gamma2[g,9];
    gamma2beta3adt[g]= gamma2[g,10];
    gamma2beta4adt[g]= gamma2[g,11];
  }
  for (n in 1:N) {
    mu_aq[n] = alphaaq + gamma1alphaaq[Group[n]] + gamma2alphaaq[Group2[n]]+
      (beta1aq+gamma1beta1aq[Group[n]]+gamma2beta1aq[Group2[n]]) * c1[n] +
      (beta2aq+gamma1beta2aq[Group[n]]+gamma2beta2aq[Group2[n]]) * c2[n];
    mu_cr[n] = alphacr + gamma1alphacr[Group[n]] + gamma2alphacr[Group2[n]]+
      (beta1cr+gamma1beta1cr[Group[n]]+gamma2beta1cr[Group2[n]]) * c1[n] +
      (beta2cr+gamma1beta2cr[Group[n]]+gamma2beta2cr[Group2[n]]) * c2[n];
    mu_adt[n] = alphaadt + gamma1alpha[Group[n]] + gamma2alpha[Group2[n]]+
      (beta1adt+gamma1beta1adt[Group[n]]+gamma2beta1adt[Group2[n]]) * c1[n] +
      (beta2adt+gamma1beta2adt[Group[n]]+gamma2beta2adt[Group2[n]]) * c2[n] +
      (beta3adt+gamma1beta3adt[Group[n]]+gamma2beta3adt[Group2[n]]) * aq[n] +
      (beta4adt+gamma1beta4adt[Group[n]]+gamma2beta4adt[Group2[n]]) * cr[n];
  }
}
model{
  sigma_alphaaq ~ student_t(5, 0, 2);
  sigma_beta1aq ~ student_t(5, 0, 2);
  sigma_beta2aq ~ student_t(5, 0, 2);
  alphaaq ~ normal(0, sigma_alphaaq);
  beta1aq ~ normal(0, sigma_beta1aq);
  beta2aq ~ normal(0, sigma_beta2aq);
  sigmaaq ~ student_t(5, 0, 2);
  sigma_alphacr ~ student_t(5, 0, 2);
  sigma_beta1cr ~ student_t(5, 0, 2);
  sigma_beta2cr ~ student_t(5, 0, 2);
  alphacr ~ normal(0, sigma_alphacr);
  beta1cr ~ normal(0, sigma_beta1cr);
  beta2cr ~ normal(0, sigma_beta2cr);
  to_vector(gamma1_raw) ~ normal(0, 1);
  to_vector(gamma2_raw) ~ normal(0, 1);
  sigmacr ~ student_t(5, 0, 2);
  sigma_alphaadt ~ student_t(5, 0, 2);
  sigma_beta1adt ~ student_t(5, 0, 2);
  sigma_beta2adt ~ student_t(5, 0, 2);
  sigma_beta3adt ~ student_t(5, 0, 2);
  sigma_beta4adt ~ student_t(5, 0, 2);
  alphaadt ~ normal(0, sigma_alphaadt);
  beta1adt ~ normal(0, sigma_beta1adt);
  beta2adt ~ normal(0, sigma_beta2adt);
  beta3adt ~ normal(0, sigma_beta3adt);
  beta4adt ~ normal(0, sigma_beta4adt);
  sigma_adt ~ student_t(5, 0, 2);
  sigma_ranef1 ~ student_t(5, 0, 2);
  sigma_ranef2 ~ student_t(5, 0, 2);
  Omega_chol1 ~ lkj_corr_cholesky(2.0);
  Omega_chol2 ~ lkj_corr_cholesky(2.0);
  aq ~ normal(mu_aq, sigmaaq);
  cr ~ normal(mu_cr, sigmacr);
  adt ~ normal(mu_adt, sigma_adt);
}
generated quantities{
  real naiveIndEffect1;
  real naiveIndEffect2;
  real naiveIndEffect3;
  real naiveIndEffect4;
  naiveIndEffect1=beta1aq * beta3adt;
  naiveIndEffect2=beta1cr * beta4adt;
  naiveIndEffect3=beta2aq * beta3adt;
  naiveIndEffect4=beta2cr * beta4adt;
}

Bob_Carpenter · February 27, 2024, 10:12pm

The low BFMI is probably coupled with some parameters having low effective sample size. I would look to those. The problem is almost always that adding new effects will provide multiple explanations for the same phenomena, which will “smear” out the posterior and add correlation, making the model harder to fit. The best way to mitigate this is through a meaningful prior. I would particularly look at the student T priors and consider replacing those with normal priors unless you are expecting big values that the student T will accomodate.

You can shrink the declarations and definitions considerably and remove the loop:

  vector[J] gamma1alphaaq = gamma1[  , 1];
  ...

and same for the mean loop, which can just be:

  vector[N] mu_aq = alphaaq + gamma1alphaaq[Group] + gamma2alphaa[Group2] + ... + (beta1aq + gamma1beta1aq[Group] + gamma2beta1aq[Group2) .* c1;

The .* is element wise multiplication and multi-indexing works the same way as in Python or R.

zrn · February 28, 2024, 8:28am

Thank you for explaining@ Bob_Carpenter！
I changed my “transformed parameters” part. I am not sure.

transformed parameters{
matrix[J, 14] gamma1 = gamma1_raw * diag_pre_multiply(sigma_ranef1, Omega_chol1)’;
matrix[G, 14] gamma2 = gamma2_raw * diag_pre_multiply(sigma_ranef2, Omega_chol2)‘;
vector[J] gamma1alphaaq = gamma1[ , 1];
vector[J] gamma1alphacr=gamma1[ , 2];
vector[J] gamma1alpha=gamma1[ , 3];
vector[J] gamma1beta1aq=gamma1[ , 4];
vector[J] gamma1beta2aq=gamma1[ , 5];
vector[J] gamma1beta1cr=gamma1[ , 6];
vector[J] gamma1beta2cr=gamma1[ , 7];
vector[J] gamma1beta1adt=gamma1[ , 8];
vector[J] gamma1beta2adt=gamma1[ , 9];
vector[J] gamma1beta3adt=gamma1[ , 10];
vector[J] gamma1beta4adt=gamma1[ , 11];
vector[J] gamma1beta3aq=gamma1[ , 12];
vector[J] gamma1beta3cr=gamma1[ , 13];
vector[J] gamma1beta5adt=gamma1[ , 14];
vector[G] gamma2alphaaq=gamma2[ , 1];
vector[G] gamma2alphacr=gamma2[ , 2];
vector[G] gamma2alpha=gamma2[ , 3];
vector[G] gamma2beta1aq=gamma2[ , 4];
vector[G] gamma2beta2aq=gamma2[ , 5];
vector[G] gamma2beta1cr=gamma2[ , 6];
vector[G] gamma2beta2cr=gamma2[ , 7];
vector[G] gamma2beta1adt=gamma2[ , 8];
vector[G] gamma2beta2adt=gamma2[ , 9];
vector[G] gamma2beta3adt=gamma2[ , 10];
vector[G] gamma2beta4adt=gamma2[ , 11];
vector[G] gamma2beta3aq=gamma2[ , 12];
vector[G] gamma2beta3cr=gamma2[ , 13];
vector[G] gamma2beta5adt=gamma2[ , 14];
vector[N] mu_aq = alphaaq + gamma1alphaaq[Group] +gamma2alphaaq[Group2] + (beta1aq + gamma1beta1aq[Group] + gamma2beta1aq[Group2]) .* c1+(beta2aq + gamma1beta2aq[Group] + gamma2beta2aq[Group2]) .* c2+(beta3aq + gamma1beta3aq[Group] + gamma2beta3aq[Group2]) .* x ;
vector[N] mu_cr = alphacr + gamma1alphacr[Group] +gamma2alphacr[Group2] + (beta1cr + gamma1beta1cr[Group] + gamma2beta1cr[Group2]) .* c1+(beta2cr + gamma1beta2cr[Group] + gamma2beta2cr[Group2]) .* c2+(beta3cr + gamma1beta3cr[Group] + gamma2beta3cr[Group2]) .* x ;
vector[N] mu_adt = alphaadt + gamma1alpha[Group] +gamma2alpha[Group2] + (beta1adt + gamma1beta1adt[Group] + gamma2beta1adt[Group2]) .* c1+(beta2adt + gamma1beta2adt[Group] + gamma2beta2adt[Group2]) .* c2+(beta3adt + gamma1beta3adt[Group] + gamma2beta3adt[Group2]) .* aq +(beta4adt + gamma1beta4adt[Group] + gamma2beta4adt[Group2]) .* cr +(beta5adt + gamma1beta5adt[Group] + gamma2beta5adt[Group2]) .* x ;
}

Topic		Replies	Views
Projpred: Interactions without marginal terms? Modeling rstanarm , projpred	12	1109	February 22, 2021
Brms: Mediation analysis or not? brms	6	1483	December 7, 2019
Logistic Regression with Interactions (ContinuousXFactors(>2Levels)) brms	13	1945	March 13, 2019
Bernoulli variables of multivariate brms model poorly estimated brms	4	672	May 7, 2019
Analyzing the interactional term in brms Modeling	1	301	January 12, 2023

Adding interactive features significantly reduces the BFMI

Related Topics