Thanks that worked.
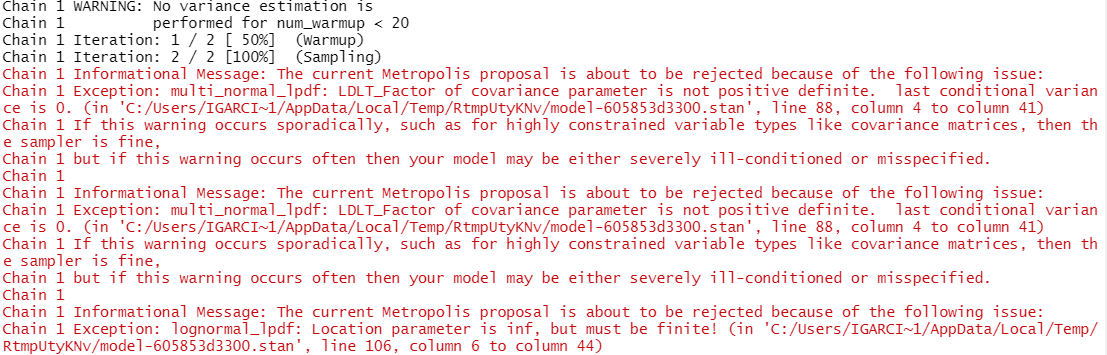
However, I am still struggling with error messages as follows:
So at least the model runs now, but I am facing divergence issues due to the specification of the variance-covariance matrix. However, I have reviewed this and try different covariance matrices but they all gave the same error message.
The code is as follows:
functions {
real[] analytic_int(real[] inits, real t0, real ts, real[] theta) {
real y[3];
real dt = ts - t0;
real C;
y[1] = inits[1]*exp(-theta[1]*dt);
y[2] = inits[2]*exp(-theta[2]*dt);
C = inits[3] + inits[1]*theta[1]/(theta[1]-theta[3]) + inits[2]*theta[2]/(theta[2]-theta[3]);
y[3] = theta[1]*y[1]/(theta[3] - theta[1]) + theta[2]*y[2]/(theta[3] - theta[2]) + C*exp(-theta[3]*dt);
return inits;
}
}
data {
int<lower=1> N;
int<lower=1> nsubjects;
int<lower=1> subj_ids[N];
real <lower=0> y[N];
int <lower=1> ntimes;
int <lower=1> nobs[nsubjects];
real ts[ntimes];
real t0;
}
transformed data {
real x_r[0];
int x_i[0];
}
parameters {
real logps;
real logpl;
real logmuab;
real sigmalogmuab;
real <lower= 0> logAB0;
real sigmalogAB0;
real logps0;
real logpl0;
real sigma;
vector[2] r[nsubjects];
//real rho_rhobit;
}
model{
real mu[ntimes, 3];
real inits[3];
real theta[3];
real new_mu[ntimes, 3];
vector[nsubjects] rAB0;
vector[nsubjects] rmuab;
real eval_time[1];
// transformed parameters
real ps = exp(logps);
real pl = exp(logpl);
real muab = exp(logmuab);
real sigma_muab = exp(sigmalogmuab);
real AB0 = exp(logAB0);
real sigma_AB0 = exp(sigmalogAB0);
real ps0 = exp(logps0);
real pl0 = exp(logpl0);
real sigmap = exp(sigma);
// defining the correlation
vector[2] mean_vec;
matrix[2,2] Sigma;
//real rho = (exp(rho_rhobit) - 1)/(exp(rho_rhobit) + 1);
//prior distributions
logps ~ normal(0, 1);
logpl ~ normal(0, 1);
logmuab ~ normal(0, 10);
sigmalogmuab ~ normal(0, 1);
logAB0 ~ normal(5, .5);
sigmalogAB0 ~ normal(0, 1);
logps0 ~ normal(0, 1);
logpl0 ~ normal(0, 1);
sigma ~ normal(0, 1);
//rho_rhobit ~ uniform(-10, 10);
//cov matrix
mean_vec[1] = -pow(sigma_AB0, 2.0)/2;
mean_vec[2] = -pow(sigma_muab, 2.0)/2;
Sigma[1,1] = pow(sigma_AB0, 2.0);
Sigma[2,2] = pow(sigma_muab, 2.0);
Sigma[1,2] = 0;
Sigma[2,1] = 0;
for (j in 1:nsubjects) {
r[j] ~ multi_normal(mean_vec, Sigma);
rAB0[j] = r[j,1];
rmuab[j] = r[j,2];
}
for (i in 1:N){
//defining the initial conditions
inits[3] = AB0*exp(rAB0[subj_ids[i]]);
inits[1] = inits[3]/ps0;
inits[2] = inits[3]/pl0;
//defining the parameters
theta[1] = ps;
theta[2] = pl;
theta[3] = muab*exp(rmuab[subj_ids[i]]);
// ode solver
mu[i] = analytic_int(inits, t0, ts[i], theta);
new_mu[i,1] = mu[i,1];
new_mu[i,2] = mu[i,2];
new_mu[i,3] = log(mu[i,3]) - pow(sigma, 2.0)/2;
y[i] ~ lognormal(new_mu[i, 3], sigma);
}
}